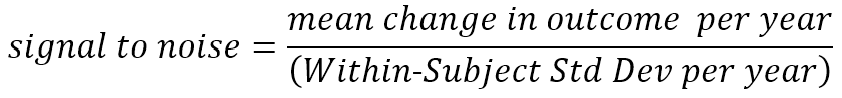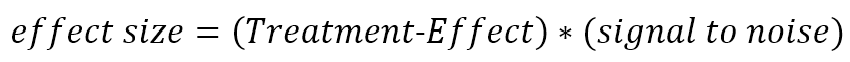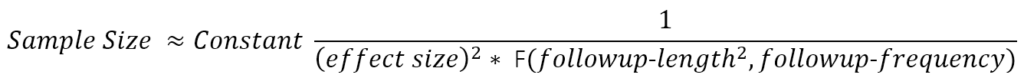Introduction

Un certain nombre de grandes études observationnelles sur la progression de la MH ont été menées au cours des deux dernières décennies (Biglan et al. 2016, Dorsey et al. 2013, Orth et al. 2011, Paulsen et al. 2014, Tabrizi et al. 2013). La plus grande de ces études, Enroll-HD (Landwehrmeyer et al. 2017), est en cours et fournit des ensembles de données librement accessibles aux chercheurs. L’objectif principal de ces études observationnelles est de fournir une meilleure compréhension de l’histoire naturelle mesurable de la MH, ce qui est nécessaire pour éclairer la conception des essais cliniques de traitements candidats visant à ralentir la progression de la maladie. Nous décrivons ici quelques considérations clés concernant les données observationnelles de MH et leur analyse qui sont particulièrement pertinentes pour la conception des essais cliniques.

L’histoire naturelle de la progression de la MH et la conception des essais cliniques

L'un des objectifs centraux de la conception des essais cliniques est de maximiser les chances de démontrer l'efficacité d'un traitement convaincant aussi efficacement que possible, en minimisant l'exposition à tout préjudice potentiel provenant d'un traitement non éprouvé, ainsi que les délais de soumission pour l'approbation d'un traitement efficace ou d'abandon d'un traitement inefficace. Cela minimise également les coûts financiers et de renonciation liés à l'évaluation d'un traitement candidat, une considération centrale lorsque l'industrie décide où et comment investir des ressources.

L'efficacité est définie comme une amélioration significative au fil du temps du taux de progression de la maladie ou du taux d'événements liés à la maladie par rapport à un groupe témoin (souvent un groupe placebo) dont l'expérience représente la progression de la maladie lorsque toutes les influences potentielles autres que le traitement sont identiques. L'expérience du groupe témoin représentera une combinaison de progression naturelle de la maladie - généralement dans le contexte de la norme de traitement actuelle - et de possibles modificateurs (par exemple, effets placebo) dus à la participation à l'essai. On s’attend généralement à ce que l’histoire naturelle soit l’influence dominante dans le groupe témoin, ce qui souligne la pertinence et l’importance des études observationnelles à partir desquelles ces effets de la maladie peuvent être mesurés puis prédits pour un futur essai clinique.

Aspects clés du changement dans la MH estimé à partir d’études observationnelles

Nous nous concentrons sur le taux de changement ou la fréquence d’apparition des phénomènes MH consécutifs. En gros, plus quelque chose change au cours du temps « X » sans traitement thérapeutique, plus il est facile de savoir si le traitement produit un effet. Si un processus évolue très lentement au fil du temps ou est très rare, alors, quel que soit son rôle central dans la MH, ce ne sera pas une mesure pratique à utiliser comme base d’un essai clinique.

Le taux de changement d’un résultat n’est pas la seule propriété de mesure importante. Les mesures qui changent rapidement en moyenne, mais qui fluctuent également énormément en raison de mesures répétées chez le même individu, peuvent être moins utiles que d'autres mesures qui changent plus lentement mais régulièrement. Cette cohérence du changement prévisible est d’une importance centrale pour déterminer la taille d’une étude nécessaire pour détecter avec confiance un effet du traitement MH (Diggle et al. 2002, Schobel et al. 2017). Le terme « rapport signal/bruit » est approprié pour désigner cet équilibre entre le taux de changement moyen prévu (signal) et la fluctuation imprévisible (bruit). Nous discuterons de ce concept crucial plus en détail ci-dessous.

L’interrelation entre la progression des mesures individuelles présente également un grand intérêt. Enroll-HD et les bases de données similaires constituent une source de données particulièrement riche pour étudier ces relations. Une grande variété de mesures sont disponibles concernant les aspects moteurs, cognitifs et psychiatriques de la maladie, ainsi que des mesures sommaires du fonctionnement quotidien. Des variables démographiques telles que le niveau d'éducation, qui ont des effets potentiellement confondants sur les relations apparentes avec la maladie, sont également disponibles.

Pour la conception des essais cliniques, les relations entre d’autres mesures et celles qui résument le fonctionnement quotidien, telles que l’échelle de capacité fonctionnelle totale (TFC) UHDRS, sont particulièrement importantes. Les régulateurs doivent être convaincus que la vie d'un patient est nettement meilleure si un traitement améliore le résultat principal de l'essai. Cependant, les résultats qui mesurent directement le « mieux », comme le TFC, ne sont peut-être pas ceux qui changent le plus rapidement et de manière prévisible. S'il existe d'autres mesures ou combinaisons de mesures pour lesquelles le changement est plus facilement détectable, une exigence supplémentaire est que ces mesures doivent au moins avoir une relation empirique forte avec des mesures telles que le TFC qui ont une signification clinique inhérente. Lorsqu’une forte relation empirique existe, nous devons finalement démontrer que ce lien entre les mesures est causal et non simplement une corrélation (Temple 1999, Burzykowski et al., 2005, US Food and Drug Administration 2018). L’amélioration de la mesure alternative se traduira-t-elle nécessairement par une amélioration cliniquement significative ?

Les études observationnelles nous permettent d’évaluer les relations empiriques entre les mesures, et il est tentant d’imputer des notions de cause à effet. Cependant, nous devons souligner qu'il est difficile de répondre à la question de la causalité sans preuves expérimentales directes (par exemple, des investigations biologiques ou des données issues d'essais cliniques antérieurs). Les analystes de données d'observation doivent être conscients qu'il existe diverses techniques statistiques qui tentent d'aborder la causalité dans les données d'observation, et celles-ci peuvent être utiles pour affiner les relations empiriques qui sont plausiblement causales. Cependant, ces techniques nécessitent également que nous acceptions diverses hypothèses fortes (et souvent invérifiables) sur la nature des données. Le recours à de telles hypothèses peut s’avérer inacceptable dans un contexte réglementaire.

Mesures pronostiques et prédiction du changement

Toutes choses étant égales par ailleurs, les effets du traitement sont plus facilement détectés avec moins de participants et sur une période plus courte parmi ceux qui présentent le changement le plus rapide et le plus cohérent dans la mesure des résultats (Langbehn et Hersch 2020). De même, si le résultat est un événement distinct tel que la perte de la capacité de vivre de manière autonome, un effet du traitement est plus facilement détecté parmi ceux qui ont la plus forte probabilité de vivre l’événement pendant la durée d’un essai clinique. Les ensembles de données d'observation tels que Enroll-HD permettent non seulement d'étudier l'évolution de la MH au fil du temps, mais également d'étudier les caractéristiques de base qui aident à prédire les changements futurs (pronostic). Dans les essais futurs, ces mesures de base pourraient être utilisées dans le cadre des critères de sélection des participants afin que l'essai soit « enrichi » pour ceux dont la maladie progressera le plus rapidement.

Nous ne devons cependant jamais supposer sans réserve que toutes les autres choses sont effectivement égales. L'avantage potentiel de l'enrichissement des essais est souvent calculé en supposant que la réponse au traitement n'est pas liée à la virulence du pronostic. Cela n’est peut-être pas vrai, et il peut souvent être plus réaliste d’envisager toute une série de relations possibles entre le pronostic et la réponse au traitement. Pour aller plus loin, dans certains cas, nous pouvons décider que les données pronostiques de base doivent être utilisées pour définir une fenêtre thérapeutique appropriée pour le traitement proposé, en excluant le dépistage de ceux pour lesquels les changements de la maladie sont susceptibles d'être trop agressifs, ainsi que pour ceux chez qui ce sera trop lent.

Même si l'enrichissement du screening n'est pas utilisé, pour de nombreux modèles d'essais, la puissance de détection d'un effet thérapeutique peut être considérablement augmentée par un contrôle statistique des caractéristiques pronostiques de base dans l'analyse des données finales de l'essai (un tel contrôle statistique doit être une caractéristique prédéfinie de l'analyse définitive de l'essai clinique.) Les caractéristiques de base peuvent expliquer (prédire) une partie du « bruit » dans les données de résultats, augmentant ainsi le rapport signal/bruit pertinent pour tester l’effet du traitement (Julious 2010). L'avantage potentiel d'un tel contrôle statistique peut être estimé à partir de données d'observation longitudinales, par exemple en étudiant la réduction d'une variation apparemment aléatoire d'un résultat lorsqu'un facteur pronostique est utilisé comme covariable dans un modèle longitudinal de progression non traitée.

Modélisation d'un sous-ensemble approprié de données d'observation

Pour que les données d’observation éclairent la conception des essais cliniques, le sous-ensemble pertinent de participants doit être choisi pour l’analyse. Ce principe de pertinence est évident à certains égards : si nous voulons modéliser un essai ciblant les premiers stades de la MH diagnostiquée, nous souhaitons alors limiter nos analyses observationnelles aux participants à ce stade précoce de la maladie. Cependant, certains aspects plus subtils de la pertinence sont parfois négligés. Par exemple, Enroll-HD contient des données de suivi longitudinales pour certains participants pendant une durée bien plus longue que la durée réaliste d'un essai clinique. En utilisant leurs données de base, il peut être approprié d'inclure ces participants dans un modèle d'essai. Cependant, après de nombreuses années, ces participants auront souvent dépassé le stade pertinent de la maladie. Nous souhaiterions donc peut-être limiter les données longitudinales analysées aux seules premières années de suivi (Langbehn et Hersch 2020). (De même, les participants ayant bénéficié d'un suivi prolongé peuvent avoir évolué vers le groupe d'étude ciblé, même s'ils auraient été exclus après avoir examiné uniquement leurs données de base. Une série d'observations ultérieures de ces participants pourrait constituer une contribution valable à l'analyse des données.)

Un (petit) peu de mathématiques.

Nous pouvons affiner notre appréciation de la pertinence des données d'observation pour la conception des essais cliniques si nous tournons brièvement notre attention vers une formule mathématique clé qui décrit les relations approximatives entre la taille de l'échantillon, la durée du suivi, l'effet du traitement et le taux de résultat d'une mesure de progression chez les non-traités. L’objectif est de comprendre que la taille de l’échantillon varie en tant que valeur au carré de caractéristiques de mesure importantes, dont deux peuvent être estimées à partir de données d’études observationnelles.

Plus tôt, nous avons fait appel à une compréhension intuitive du terme rapport signal sur bruit. Nous définissons maintenant plus précisément ce que nous entendons par ce terme. Nous faisons ici référence au changement par an, mais la définition peut être appliquée à toute unité appropriée de temps de suivi.

Le signal que nous souhaitons détecter (et espérons changer grâce à une thérapie) est la quantité moyenne de (vrai) changement se produisant au fil du temps. Le bruit, au dénominateur, reflète l'écart imprévisible autour du taux de changement moyen de chaque participant ; ce bruit est parfois appelé erreur de mesure, mais ce terme peut être trompeur (dans ce contexte, le bruit inclut également des écarts réels à court terme par rapport à la tendance moyenne à long terme, par exemple, les signes moteurs d'un HDGEC varient quelque peu d'un jour à l'autre autour de leur moyenne à court terme ; la variation des scores moteurs UHDRS enregistrés qui reflètent parfaitement cette variation réelle autour de l'augmentation du score moteur moyen est néanmoins considérée comme du bruit pour nos besoins.) En l'absence de données substantielles d'essais cliniques antérieurs, ce rapport signal sur bruit est estimée à partir de données d'observation longitudinales obtenues dans des études telles que Enroll-HD. (Il est le plus souvent calculé à l’aide des estimations des composantes d’effet fixe et de variance d’un modèle longitudinal à effets mixtes de ces données).

Le facteur par lequel un traitement modifie le taux moyen de déclin se reflète dans l’ampleur de l’effet du traitement.

Par exemple, si un groupe de traitement a connu une baisse moyenne du TFC de 0,6 point par an et que la baisse moyenne du groupe témoin était de 1,2 point par an, alors l'effet du traitement serait de 0,6/1,2 = 0,5. La traduction de l'effet du traitement en taille de l'effet traduit l'ampleur de l'effet du traitement en unités d'écarts types au sein des participants. Il s'agit de l'unité de mesure qui détermine la taille de l'échantillon pour un essai clinique. Dans l’exemple ci-dessus, supposons en outre que l’écart type d’une année sur l’autre du changement de TFC chez les individus est de 0,8 point par an. Le rapport signal sur bruit (non traité) est alors de 1,2/0,8 = 1,5. La taille de l'effet du traitement est de 0,5 * 1,5 = 0,75.

Prenons l’exemple d’un essai randomisé à deux bras comparant l’effet du traitement à celui d’un placebo. Le résultat de l'essai est un changement induit par le traitement dans le taux de progression de la mesure des résultats. La formule approximative de la taille de l’échantillon a la forme suivante :

La fonction F(.) au dénominateur fournit une valeur qui augmente approximativement avec le nombre et l'espacement des visites de suivi au cours desquelles le résultat est évalué et, plus important encore, avec le carré de la durée totale du suivi (Diggle et al.2002). (F(.) est la somme des carrés des durées de visite moyennes ajustées.) Cette formule est approximative mais illustre des relations qui restent fondamentales dans des calculs plus détaillés qui reflètent mieux les détails réalistes des essais (Julious 2010) (par exemple, effets placebo, taux de sorties d'étude, essai à bras multiples et conceptions adaptatives à l'analyse intermédiaire.). La durée et la fréquence du suivi sont définies par les concepteurs de l'essai. L’effet thérapeutique cliniquement significatif que l’on espère détecter est une question de conjecture (espérons-le bien argumentée). Cela laisse le rapport signal/bruit de la mesure des résultats comme quantité critique à estimer à partir des données historiques. Les données recueillies dans le cadre d’études observationnelles longitudinales et prospectives seront souvent les données les mieux adaptées pour obtenir ces estimations.
Notre cache toujours croissant de données de ce type, collectées à partir d’études telles que Enroll-HD, fait de la MH l’une des maladies cérébrales les plus soigneusement documentées. À terme, l'expérience prospective des essais MH permettra d'estimer des paramètres secondaires importants tels que les effets placebo et les biais induits par les attentes des évaluateurs. La plupart de ces essais doivent encore être conçus, et ces conceptions dépendront essentiellement des données d'observation existantes telles que celles discutées ici.

Les références

Biglan KM, Shoulson I, Kieburtz K et al. Associations clinico-génétiques dans l'étude observationnelle prospective Huntington at Risk (PHAROS) : implications pour les essais cliniques. JAMA Neurol 2016;73(1):102-110.

Burzykowski T, Molenberghs G, Buyse M. L'évaluation des paramètres de substitution. Springer, New York. 2005.

Diggle P, Heagerty P, Lian K, Zeger S Analysis of Longitudinal Data, deuxième édition. Presse de l'Université d'Oxford. Oxford Royaume-Uni. 2002

Dorsey ER, Beck CA, Darwin K, Nichols P, Brocht AF, Biglan KM, Shoulson I ; Enquêteurs du groupe d'étude Huntington COHORT. Histoire naturelle de la maladie de Huntington. JAMA Neurol. Décembre 2013;70(12):1520-30. est ce que je: 10.1001/jamaneurol.2013.4408.

Julius SA. Tailles des échantillons pour les essais cliniques. Presse CRC. Boca Raton, Floride. 2010.

Landwehrmeyer GB, Fitzer-Attas CJ, Giuliano JD, Gonçalves N, Anderson KE, Cardoso F, Ferreira JJ, Mestre TA, Stout JC, Sampaio C. Data Analytics de Enroll-HD, une plateforme mondiale de recherche clinique sur la maladie de Huntington. Mov Disord Clin Pratique. 22 juin 2016;4(2):212-224. est ce que je: 10.1002/mdc3.12388. eCollection 2017 mars-avril.